Ultrasonic Resonator Design
Using Finite Element Analysis (FEA)

Table of Contents

Abstract

This paper discusses the methods, advantages, and limitations of finite element analysis for the design of ultrasonic resonators (resonators/sonotrodes/probes, boosters, and transducers/converters) for power ultrasonics. Typical examples are given.

This paper was originally presented at the Ultrasonic Industry Association's 1991 technical symposium, when it was  titled "The Application of Finite Element Analysis to the Design of Ultrasonic Resonators".  It has been updated to reflect current practices.

Overview

Finite element analysis (FEA) is a computer-based method for analyzing and improving resonator performance. (Note: FEA is sometimes called FEM -- finite element method.) In FEA, the resonator is simulated as a computer model.  The computer simulation model consists of a large number of small "elements" that represent (approximately) the shape of the resonator. Each element can be described mathematically by a set of equations.  The solution to this set of equations yields a prediction of the resonator's performance -- i.e., the natural frequencies at which the resonator will vibrate and the amplitudes and stresses associated with each of these frequencies.   After the performance has been predicted, the resonator's dimensions or materials can be changed within the FEA model in order to improve the performance.

The following discussion will emphasize FEA of medical probes, as used phaco emulsification (cataract surgery) and similar applications. However, FEA is equally applicable to the design of industrial resonators. For examples, including animations, see bar horns, block horns, cylindrical horns, and boosters.

Notes:

1. The resonators discussed below have a nominal axial resonance of 25 kHz, although any design frequency is possible.
     
2. See the glossary for definitions and symbols.

Requirements for Adequate Resonator Design

In order for a resonator to function properly, consideration must be given to the following performance factors.

1. Primary resonance tuning. The frequency of the primary (desired) resonance must be adjusted to the nominal resonance of the power supply (generator). This frequency must account for the expected operating temperature of the resonant stack.
     
2. Secondary resonance tuning. The resonator must have sufficient frequency separation between the primary and all secondary (undesired) resonances. Otherwise, the power supply may accidentally "jump" to a secondary resonance, especially during the transient starting conditions or under highly loaded conditions. Such a jump could cause poor or erratic performance and could overstress the resonator. Poor frequency separation may also cause nonuniform or asymmetric resonator amplitudes, which may lead to early transducer failure.
     
3. Gain. The resonator must have sufficient gain (output amplitude) to perform the application.
     
4. Amplitude uniformity. The amplitude at the resonator's face must be sufficiently uniform to perform the application. The amplitude at the resonator's input surface must be sufficiently uniform to prevent heating and galling at the joint interface.  (These requirements apply mainly to industrial horns, whose face and input surfaces may be relatively large and are therefore prone to significant amplitude variations over these surfaces.)
     
5. Amplitude direction. The predominate amplitude should be in the desired direction in order to maximize the effectiveness of the ultrasonics while minimizing undesired side effects (heating, scrubbing, wasted power, etc.). The desired direction is generally along the axis of the resonator, although there are notable exceptions -- e.g., radial resonators (disks and tubes) or flexural resonators (plates, strips, disks, tubes, dental prophylaxis probes, etc.).
     
6. Node location. If the resonator is to be mounted at a node, then the mounting flange must be properly positioned at the node so that minimum energy is transmitted to the support structure.
     
7. Stress. The stresses must be sufficiently low for long resonator life.
     
8. Loss. The loss must be low to avoid associated problems (thermal runaway in piezoelectric ceramics, tissue heating, operator discomfort in handheld devices, etc.).
     
9. Starting. The resonator must achieve the operating amplitude within the time permitted by the power supply. Thus, the energy distribution within the resonator and between the resonator and booster must be considered.
     

In addition to these performance considerations, the following must also be considered.

1. Materials. Materials must give adequate fatigue and wear/erosion life. For medical probes, the materials that are in contact with tissue must not cause detrimental effects; also, the materials and design must be amienable to sterilization, if required.
     
2. Geometry constraints. The resonator must fit within a geometry envelope. For a handheld medical probe, the probe must be lightweight and relatively slender.   For plastic welding horns, the horn must conform to the shape of the part.
     
3. Maunfacturability.  The resonator must be manufacturable at reasonable cost.

Conventional Resonator Design

First, consider the conventional approach to resonator design.

1. Design the resonator. The resonator's design is based on the engineer's experience and best judgement.
     
2. Machine and tune the resonator to the desired frequency. Care must be taken not to mistune or tune to a nonprimary resonance.
     
3. Evaluate the resonator performance. Determine if the resonator meets the performance requirements.
     
4. Correct the known problems. If the resonator's performance is not acceptable, then modify the existing resonator and repeat step 3 or, if required, start again from step 1.
     
5. Ship the resonator. Wait for the customer to find additional problems (usually fatigue failure) associated with extended use.
     
6. Correct the customer's problems. Start over from step 1.

There are at least two problems with this approach.

1. This cut-and-try approach wastes time and material. The resonator performance parameters cannot be determined until a prototype resonator has been machined. If the prototype resonator does not have adequate performance or if it cannot be remachined to achieve adequate performance, then additional resonators may be required. This rework creates scheduling difficulties and delays delivery.
     
2. Resonator reliability will be difficult to estimate. This is because certain performance parameters cannot be easily evaluated. For example, there is usually no convenient way to determine resonator stresses, so estimates of resonator life will be crude. (Note: even if holographic or thermographic equipment is used for stress measurement, this equipment will only show surface stresses, not the internal stresses which may be most critical.) Similarly, amplitudes at the joints (e.g., between the resonator and booster) will be impossible to measure, so joint problems will be difficult to detect. Thus, evaluation of resonator reliability is often left to the customer.

FEA Resonator Design

Unlike conventional resonator design, FEA attempts to solve the performance problems before the resonator is machined. The process has eight steps.

1. Specify the performance factors
2. Establish the material properties
3. Model the resonator
4. Process the model
5. Evaluate
6. Iterate
7. Machine and tune the resonator
8. Verify the performance

These steps may be applied to a conceptual resonator whose performance is unknown or to an existing resonator whose performance is inadequate.

The following steps will be illustrated with a medical probe (figure 1) whose primary axial resonance is at 25 kHz. The probe is driven by a power supply (generator) which delivers electrical energy to the piezoelectric ceramics. This causes the ceramics (and, hence, the probe) to expand and contract at the probe's resonant frequency.

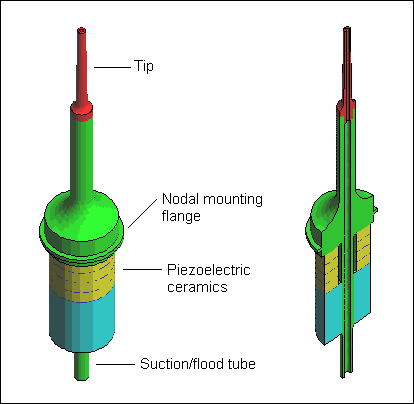
Figure 1. Typical medical probe.
     Left: full model
     Right: sectioned model
  

Specify the performance factors

The engineer must first decide what performance factors are important for the particular resonator. This will dictate certain requirements for the computer model, which will determine the time needed to complete the FEA. See Requirements for Adequate Resonator Design.

(Specifics are discussed in the section Modeling Considerations.)

Establish the material properties

The engineer must establish the material properties that will be used for subsequent FEA. These properties can be determined from ultrasonic tests or static tests, or, less preferably, can be estimated from handbook values.

Alternately, the engineer can run a preliminary FEA (as described in the following sections) on an existing resonator that has the same material and similar dimensions to the conceptual resonator. The material properties are then adjusted until FEA adequately predicts the measured performance of the existing resonator.

Model the resonator

During the modeling phase, the engineer constructs an idealized computer model of the actual resonator. The model is composed of a large number of small elements that are sufficient to describe the geometry of the resonator. This is called "creating the mesh". The mesh intersections are called nodes. The mesh elements must be sufficiently small that the solution for the desired results will converge. (See section on Modeling Considerations.) The previously determined material properties are also specified.

In the following figure, only half of the resonator has been modeled because of axial symmetry. By reducing the number of elements, the analysis time is significantly reduced.

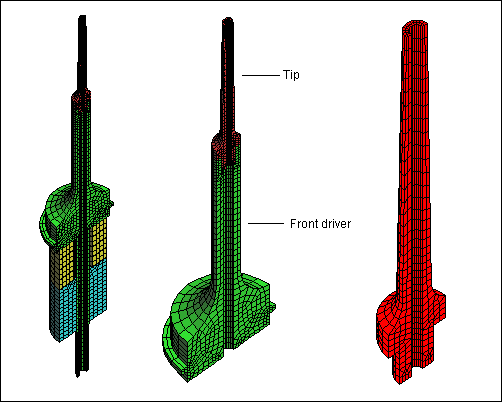
Figure 2. Resonator model (1/2 section) with element mesh (black lines)
     Left: Complete resonator
     Middle: Enlarged view of tip and front driver
     Right: Enlarged view of tip
  

Depending on the model, the engineer may also have to apply certain boundary conditions so that the model will not vibrate in unrealistic directions.

Most FEA programs have CAD-like preprocessors that aid in constructing the model and the mesh.

Process the model

Once the model has been completed and verified, it is submitted for processing.   The computer solves the required equations and outputs the results.

Evaluate

When the processing is complete, the engineer must check the output to determine if the predicted resonator performance is acceptable (e.g., uniformities, stresses, frequency separation, etc.). The following figures show typical results.

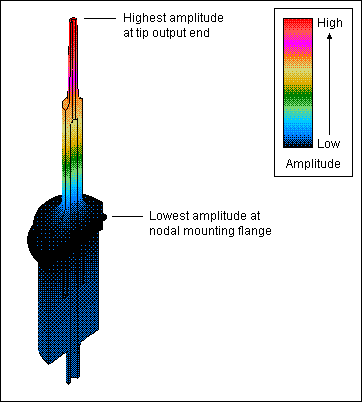
Figure 3. Axial mode at 25.0 kHz: relative amplitudes
  

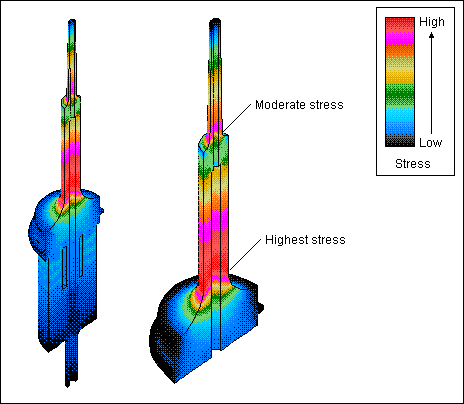
Figure 4. Axial mode at 25.0 kHz: relative stresses.
     Left: Complete resonator
     Right: Enlarged view of tip and front driver
  

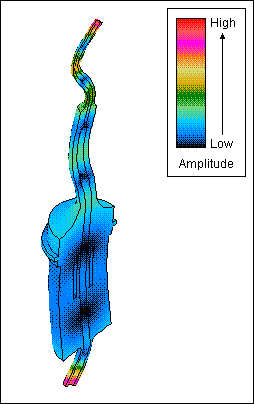
Figure 5. Bending mode at 23.8 kHz: relative amplitudes.
  

Iterate

If the resonator performance is not acceptable, then the engineer must return to the modeling phase and adjust the resonator dimensions. The revised model is then submitted for processing. This process continues until adequate resonator performance has been achieved, or until no further performance improvement seems possible.

Machine and tune the resonator

After the performance of the FEA model has been correctly adjusted, a resonator is machined to the dimensions of the FEA model. The resonator is then tuned to the specified frequency.

Verify the performance

If the FEA has been performed properly, then the performance predicted by FEA should agree reasonably with the actual resonator performance. Agreement should be especially good if similar resonators have been previously modeled. Exact agreement should not be expected, either because of limitations of the FEA or because of measurement errors for the actual resonator.

Frequencies

Frequencies are easiest and most accurate parameter to measure and verify. However, note that FEA may predict more frequencies than can be measured in the actual resonator. These extra FEA frequencies are often bending resonances or resonances where a node that runs through the resonator's axis. Although such frequencies are actually present in the resonator, they often cannot be easily excited by the transducer and are therefore difficult to detect by frequency analyzer equipment. Although these extra resonances can often be ignored, they can sometimes interact with the primary resonance, causing asymmetric amplitudes and high stress.

In some cases, the extra FEA frequencies are caused by boundary conditions that are needed to constrain the FEA model. Such FEA frequencies are erroneous and will not exist in the actual resonator. It is the responsibility of the FEA engineer to recognize this situation.

Amplitudes

Amplitudes are relatively easy to verify, but care must be taken to assure that the amplitudes and their locations are correctly measured. This is especially important where the amplitude changes rapidly (e.g., at the edge of large-diameter unshaped cylindrical resonators). Depending on the sophistication of the amplitude measurement equipment and the care of the operator, 5% amplitude difference between the measured values and the FEA values would not be unusual.

If the FEA frequencies or amplitudes have larger error than expected, this may indicate improper modeling (e.g., not enough of the resonator or improper boundary conditions), inadequate mesh refinement, incorrect material properties, or incorrect measurements.

Stress

Since empirical stress data is usually not available, stress usually cannot be directly verified. However, the FEA stresses will not be correct if the FEA amplitudes are not correct, since stress depends on the amplitude gradient. Even if the FEA amplitudes are correct, the FEA stress may still be incorrect due to poor choice of element sizes or geometry. Some FEA programs permit estimates of FEA stress error and indicate where the mesh needs to be refined to reduce the error.

The inability to verify FEA stresses may not be a problem, since the FEA engineer may not be concerned with absolute stress values; he may only want to know if the stresses have improved between successive FEA designs. This is especially true where the fatigue properties of the resonator material are unknown, in which case the resonator life cannot be predicted anyway. (See the section on Technical Limitations of FEA/ Predicting resonator Life.)

Application of FEA

From the above discussion, the advantages of FEA are apparent. Compared to conventional resonator design, FEA permits a substantially complete resonator design before any machining begins. Because FEA gives information that is not available with conventional resonator design, the resonator performance can be optimized to an extent that would not otherwise be possible. FEA can indicate potential performance problems and, if these cannot be corrected, subsequent reliability testing can focus on these problems.

The use of FEA must be balanced against the payback. The main constraint on FEA is the time required to input the initial FEA model, where the modeling time grows exponentially with the complexity of the resonator, and the time required to optimize the design. Thus, FEA can best be used in the following situations.

Resonator life is critical

If the customer has an application where resonator failure and replacement would be costly (e.g., in an automated assembly line) or might result in injury (e.g., medical   probes), then the resonator must be designed for maximum life. FEA allows internal resonator stresses to be analyzed and minimized before the resonator is machined. If the "optimized" stress still appears too high, the application may be redesigned to permit use with resonators of lower stress. If this is not possible, then the customer can be informed of the risks, and the resonator can be given the appropriate warrantee.

The resonator will be produced in large quantities

Such high volume resonators (transducers, boosters, certain resonators) can be analyzed to optimize the design. The resulting FEA cost per resonator is small.

Empirical design would be too costly

Certain resonator modifications do not lend themselves to cut-and-try methods. For example, if a resonator will use angled slots for improved uniformity, it would certainly be more cost-effective to analyze different slot angles by FEA than by machining many different resonators, each with a different slot angle. FEA can also provide information on stresses, which would not be available through cut-and-try.

Empirical design would not provide the needed information

Even after machining, the actual resonator may not provide the information that is needed to evaluate its performance.

Stresses

With conventional resonator design, surface stresses can be measured after the resonator has been made, although this requires sophisticated test equipment. In contrast, FEA can predict both static and dynamic internal stresses before the resonator has been made. For example, if any of the stresses in figure 4 had been excessive, then this resonator could have been redesigned to reduce these stresses. If the fatigue characteristics of the material are known, then the resonator life can be estimated.

Amplitudes

FEA can predict ultrasonic amplitudes throughout the resonator. This can be useful for determining node locations on boosters and transducers (figure 3). It can also be used to determine the amplitudes at inaccessible location (e.g., the amplitudes across interfaces such as horn-booster joints and ceramic interfaces). This can provide insight into problems such as interface heating and galling.

In addition, FEA can predict amplitudes that cannot be easily measured. For example, FEA can predict the transverse amplitudes on the face of a horn, which may cause scrubbing problems or excessive transverse vibration of attached pins (as used for ultrasonic machining of ceramics). Many measurement devices (e.g., lasers) cannot measure such amplitudes.

Modes

FEA can predict asymmetric modes that cannot be readily detected by spectrum analyzers (figure 5). As discussed above in the section on verifying the performance, these modes can interact with the axial resonance, causing asymmetric amplitudes and high stress in the axial mode. Early detection by FEA allows these frequencies to be repositioned with respect the axial resonance, so that their effects are reduced.

Empirical design is too variable

In certain circumstances, the variability of empirically measured data masks the effects of design changes. For example, when machining a transducer to improve its performance, the transducer must often be disassembled between each machining operation. However, each disassembly-reassembly operation introduces additional variables ("noise") which can obscure the effect of the machining operations.

Variability of empirical data also occurs from variability of material properties. For transducers, variability is caused by differing ceramic performance. In titanium, variability may occur between batches of material.

FEA eliminates these kinds of variability problems. With FEA, the effects of any design changes are exactly repeatable and all performance changes can be directly attributed to design changes.

Technical Limitations of FEA

While FEA could conceivably be used to model almost any resonator, it will not be practical or cost-effective in all situations. The following are general limitations which may be overcome in specific instances.

Modeling limitations

Some of FEA's limitations arise from difficulties in creating an adequate model of the resonator. This is especially true for resonators with complex geometries (e.g., heavily contoured resonators or composite resonators) that require three-dimensional models.

As discussed in the section on Modeling Considerations, the model is often simplified in order to reduce modeling and computing time. Such a model will always give somewhat limited or incomplete results. The FEA engineer must have sufficient experience to estimate the effect of such simplifications.

Predicting resonator life

FEA can predict resonator stresses. However, resonator stresses do not allow life predictions unless the fatigue characteristics of the resonator material are known. Unfortunately, there are significant problems in determining fatigue characteristics. Fatigue can be affected by the frequency of vibration, so that conventional (low frequency) handbook data may not predict the fatigue at ultrasonic frequencies. Even where it might be reliable, low frequency data is usually too limited to provide life predictions at ultrasonic frequencies. For example, low frequency tests are often stopped at 500 million cycles, which represent only seven hours of continuous ultrasonics at 20 kHz.

Further, fatigue is affected by the raw stock type (rod, bar, or plate), the raw stock size, and the direction of vibration relative to the material's grain. For nominally equivalent material, fatigue may also vary from heat-to-heat (especially for titanium) or among different manufacturers.

Fatigue is also affected by machining, which can leave residual tensile stresses that shorten resonator life. These stresses are difficult to predict, since they depend on such factors as material removal rate, the type of machining coolant, the tool sharpness, etc. FEA cannot predict these surface stresses.

Thus, unless the material's fatigue properties and the effects of machining are well known, the stresses predicted by FEA probably cannot be used to predict resonator life. However, the FEA stress data can be used to redesign resonators that have known failure problems.

Note: although this is listed as a limitation of FEA, it is also a limitation of any other method of resonator analysis. The resonator life cannot be predicted from stress unless the material's fatigue characteristics are known.

Predicting joint problems

In most cases, joints are simply modeled as if the joined components were welded together. Although this approach works well in predicting most performance factors, it does not allow prediction of joint problems arising from fretting or slippage.

Such joint problems can occur at the booster-resonator joint because of nonuniform amplitude at the interface. Joint problems can also occur in the transducer because of flexing resonators or because of inadequate ceramic clamp force. Other joint problems occur at threads (e.g., for tips, studs, transducer stack bolt).

In order to model such joint problems, the joint friction must be known. However, this friction may change with time as joint fretting progresses.

In some cases joint problems can be predicted based on amplitudes and uniformities at the joint, but the extent of the problem can only be determined when the actual resonator is tested.

Predicting stack loss

Stack loss includes the material loss of the resonator, booster, and transducer, the radiated air loss, and the frictional loss at the stack joints. If the FEA program calculates the stored energy of the model, then the resonator and booster material loss can be calculated if their material's Q's are known. (Q is a material property that relates the energy stored to the energy dissipated per cycle.) The material loss of the transducer is much more difficult to estimate (see below). Prediction of radiated air loss may be possible by FEA. As previously discussed, FEA cannot reasonably predict frictional loss, especially loss caused by flexure.

Predicting performance under load

FEA can predict the performance of a resonator under load. However, the analysis may be extremely difficult. This is because the load may have nonlinear characteristics and the load's characteristics may change as the ultrasonic process progresses. This would be true, for example, in plastic welding and metal welding. Because of these problems, the effect of the load is generally ignored during resonator design.

Although a FEA frequency response analysis can give some insight, FEA cannot predict power supply starting problems or the tendency of the power supply to jump to a nonprimary resonance under heavy load.

Predicting bending modes

FEA can predict bending modes. However, in order to do so, the entire resonator stack must be modeled. For example, to analyze the bending modes for a plastic welding stack, the horn-booster-transducer assembly would have to be modeled. Compared to modeling a single component (typically the horn), this causes the following problems.

1. The modeling time may be much longer. This is because extra components (e.g., the booster and transducer) must be added to the model. In addition, the complexity of the model may increase. For example, where an axisymmetric model might normally be used, extraction of bending modes will require a 1/2 3-D model (minimum).
     
2. The analysis time will be much longer. With the added components, the size of the model (number of elements) increases. Also, the number of extracted modes increases.
     
3. Bending modes depend on the stack components. If a stack is analyzed with a particular transducer-booster, then the bending modes will change if another transducer or booster is substituted. Since horns are often required to run with several different boosters or transducers, analysis of all possible combinations is usually not practical.

Also, in those cases where the bending involves microslip of the transducer's ceramics (a nonlinear phenomenon), the FEA predictions may not be accurate. Thus, unless bending modes are suspected of causing problems, they are often ignored, especially in the initial analysis.

Predicting transducer characteristics

Unless the FEA program contains an element type that describes the operating characteristics of piezoelectric ceramic, it cannot predict the output amplitude of a transducer due to a specified electrical input.

FEA can analyze heat transfer problems. However, FEA has limited ability to predict transducer temperatures. This is because the heat generation within ceramics depends on many factors (e.g., the drive voltage, the load, the ceramic age, the time since the transducer was assembled, the static preload, the insulation used on the ceramics to prevent arcing, variations among ceramics, microslippage at ceramic interfaces, etc.). These factors make it difficult to accurately characterize transducer heating.

Despite these limitations, FEA is still useful in transducer design. FEA can predict static preload stresses , resonant frequencies, the node location , the relative amplitude distribution, and stresses relative to the output amplitude. See figures 3, 4, and 5.

Administrative Limitations of FEA

Optimization

If the purpose of the FEA is to analyze an existing resonator design, then this can usually be done within several days. Obviously, the time required will depend on the complexity of the resonator and the complexity (or degree of simplification) of the FEA model.

However, if the purpose of the FEA is to improve (optimize) the performance of a resonator, then the time required can be considerably longer. The time required will depend on the complexity of the resonator and the model, the number of performance factors that must be improved (e.g., uniformity, stress, gain, etc.), the degree of improvement required, and the acoustic engineer's knowledge about how to resolve the resonator's problems. The resonator design must be repeatedly altered and rerun until an acceptable design has been achieved.

A difficult resonator may require a week or more to optimize (excluding the time needed to actually make the prototype resonator and verify the FEA performance). Even with this effort, the results may not meet the optimization goals. Sufficient time must be allocated for this optimization process.

Modeling Considerations

In order to properly compare FEA to conventional resonator design, the considerations for developing the computer FEA model must be understood.

The FEA model is a computer approximation of an actual resonator. The error of this approximation will depend on the refinement of the model. Although refined models give better results, they require more engineering and computing time. The degree of refinement will depend on two factors.

1. Selection of performance factors. The engineer must decide what resonator performance factors (frequencies, amplitudes, stresses) are important for a particular resonator design. The engineer then constructs an FEA model which will adequately predict the specified performance factors.
     
2. Convergence requirements. The FEA results will converge to a solution as the mesh is refined and as the mesh more closely approximates the actual resonator geometry. (Note: convergence does not necessarily imply accuracy.)

Performance factors

Frequencies

The refinement of the FEA model will depend on which modeshapes are considered important. Flexure (bending) modes depend on the dimensions of the entire stack (resonator + booster + transducer). Therefore, if flexure modes are important then the entire stack must be modeled in three dimensions. Unless the stack is axisymmetric, the required model may be very time consuming to develop.

Even if such a 3-D model was developed, it would have limited usefulness in predicting flexure. First, flexure modes may involve slip of the transducer ceramics and will, therefore, be amplitude dependent (nonlinear). This will preclude correct prediction of flexure frequencies. Second, flexure modes depend on the specific stack components. If the customer uses a different booster or transducer than was originally modeled, then the model will not predict the customer's flexure resonances. Thus, flexure resonances (which seldom cause problems in actual practice) are generally ignored during initial FEA.

If the flexure modes can be neglected, then reasonable frequency accuracy can usually be achieved by modeling only the resonator (i.e., no transducer or booster). Further, if the resonator is symmetric and certain asymmetric modes can be ignored, then further simplifications of the model are possible. Cylindrical resonators which are symmetric about their stud axis can often be modeled axisymmetrically (a two-dimensional approximation).

While modeling only a section of the resonator will save modeling and computing time, it also limits the FEA results, since asymmetric modes may not be extracted. For example, a 20 kHz 100 mm diameter unshaped cylindrical resonator will have a asymmetric "shear" resonance adjacent to the axial resonance, which will cause significant amplitude asymmetry for the axial resonance. Neither an axisymmetric model nor a 1/2 3-D model would predict the asymmetric resonance; only a full three-dimensional model could do so. Of course, the three-dimensional model is more difficult to design and more time-consuming to run.

All resonators will have flexure and asymmetric modes. A limited FEA model that precludes these modes can lead to unexpected problems when the actual resonator is machined. Unfortunately, the effect of these modes on resonator performance cannot usually be predicted in advance. In some cases, however, experience with previous resonators can provide some guidance.

Amplitudes

The sophistication of the FEA model will depend on which amplitudes need to be predicted. For example, axisymmetric models predict amplitudes across the resonator diameter, but not around the resonator's circumference. If circumferential amplitudes are important, then a 3-D model is required.

Stress

If the engineer is confident that the resonator will not fail, then FEA does not have to give accurate stress predictions. This can considerably simplify the FEA model.

For example, if stresses are unimportant, then slots can approximated as rectangles with "square" ends, rather than rounded ends. This approximation will have little effect on the resonant frequencies or amplitudes. However, such a model could not possibly predict the stresses at the slot ends.

If the resonator stresses are important, then the slots would have to be modeled with rounded ends, which could significantly increase the modeling time. This is because the mesh at the rounded ends may need to be adjusted by hand, especially at slot intersections. The computing time also increases because of the increased number of elements needed to model the rounded slot.

Convergence requirements

FEA estimates the performance of the actual resonator. As the size of the FEA elements is reduced (i.e., as the mesh is refined), each performance factor will converge to its terminal value. The rate of convergence will depend on the particular performance factor and on the skill used to refine the mesh. Note: convergence does not necessarily imply accuracy.

Frequencies and amplitudes

Generally, the frequencies converge most quickly their final values; amplitudes converge more slowly.

Stress

Stress, which depends on the gradient of the amplitude (i.e., the strain), may require a much finer mesh, especially at stress concentrations (e.g., at radii, slot ends, etc.). The required mesh size for stress convergence will depend on the geometry of the particular stress concentrator. Some FEA programs provide estimates of stress error, which indicates where the mesh must be refined to reduce the stress error. (These estimates of stress error assume that the frequencies and amplitudes have essentially converged.)

Thus, consideration of performance and convergence will determine the complexity of the model. As the complexity increases, both modeling time and computing time may increase substantially. Thus, the model should be kept as simple as possible, consistent with the desired results. As discussed above, however, the required degree of simplicity cannot always be judged in advance.

The usual approach is to model the resonator in the simplest manner that the engineer deems prudent. This requires good familiarity with both FEA and ultrasonic resonators. If the FEA results do not adequately predict the frequencies or amplitudes of the machined resonator, then a more sophisticated model will be needed.

FEA Accuracy

FEA will not be useful unless it gives accurate results. As discussed previously, the user must be sure that the FEA solution has converged. However, a converged solution does not necessarily imply an accurate solution. Accuracy will depend on several factors.

Material properties

FEA cannot correctly predict resonator performance unless the resonator's material properties (Young's modulus, modulus of rigidity, Poisson's ratio, and density) are known. For resonators with small lateral dimensions, the density and the modulus of elasticity (which determine the thin-wire wave speed) determine the resonant frequencies. The axial frequency of a 20 kHz resonator will change by 100 Hz for every 1% error in the modulus of elasticity or density.

For larger resonators, the resonant frequencies are affected somewhat by Poisson's ratio. Depending on the resonator's shape, the amplitude can also be significantly affected by Poisson's ratio.

For materials that are reasonably isotropic (e.g., most aluminums), only two elastic property values are needed to completely characterize the material. These properties are relatively easy to determine. For materials such as titanium and piezoelectric ceramics that are orthotropic (i.e, the properties depend on the test direction), nine elastic property values are needed for complete characterization. However, using averaged material values (i.e., assuming that titanium is isotropic) usually gives reasonable results. A further problem with titanium is that its properties may vary from batch to batch and may also depend on the size of the raw stock.

Where resonator frequencies are concerned, a small error in the material properties is usually not critical, since most resonators allow some extra material for tuning. However, fixed-length resonators (e.g., transducers and boosters) do not enjoy this allowance.

In general, then, some FEA error should be expected due to inexact material values.

Modeling fidelity

The FEA model must accurately represent the actual acoustic system. This means that the geometry must be correctly modeled and boundary conditions must be correctly enforced.

Geometry

The model geometry should reasonably approximate the actual acoustic system. (See the section Modeling Considerations for further discussion of modeling fidelity.)

Sometimes a seemingly insignificant change in geometry can dramatically affect the FEA predictions of resonator performance. For example, omitting a stud from a horn with large lateral dimensions (e.g., block horns, spool horns, etc.) can significantly affect the amplitudes and stresses, although the effect on resonant frequencies may be minor.

Effect of transducer-booster

The transducer-booster components usually do not have a significant effect on the primary mode. However, these components can significantly affect the frequencies predicted for other modes. (See Predicting bending modes.) Therefore, if the horn is modeled without the transducer-booster, then the optimized FEA design must allow extra frequency separation between the primary and nonprimary modes in order to compensate for this potential error.

Note: even in the primary mode, the transducer-booster may have an effect if the interfaces are not properly designed. For example, this can occur when a transducer-booster is attached to a flexing disk if the disk has significant bending across the interface joint.

Method of analysis

In order to determine the effects of adjacent resonances on the primary resonance, an estimate of the damping (Q) at each natural frequency will be needed. However, such damping estimates are imprecise, often because the damping characteristics of the transducer may not be well known. This will introduce some error, especially when the damping is high (low Q).

Accuracy estimates

If the resonator has been properly modeled and the solution has converged and the material property values are accurate, then FEA frequencies and amplitudes are usually within several percent of the measured (empirical) values. FEA gain is usually within 5% of measured values.

Remember, however, a measured value is not necessarily an accurate value. This is especially true for gain measurements, which involve indirect measurement of the resonator input amplitude. Thus, disagreement between empirical measurements and FEA values does not necessarily mean that the FEA values are incorrect.

Conclusion

This paper has described the advantages and limitations of FEA as compared to conventional resonator design. As with any tool, FEA is not appropriate for all occasions. However, for those occasions that warrant its use, FEA can provide insight and design opportunities that would otherwise be impossible.

If you have a resonator design that might be improved by finite element analysis, then you can use the Resonator Information Form to submit baseline information or you can contact Krell Engineering directly.

Glossary and symbols

3-D -- three-dimensional.

asymmetric resonance -- a resonance in which the amplitudes are different at symmetric locations on the resonator.  

asymmetry -- an aberrant condition in which vibration motion at two or more geometrically identical locations (e.g., the four corners of a block horn) are not identical (within measurement tolerance). This may occur with resonators that have large lateral dimensions (e.g., bar horns and block horns), particularly if a nonprimary resonance interferes with the primary resonance. Generally, the optimum asymmetry is 0. (Also see Uniformity.)  

axial resonance -- a resonance where the major amplitudes are generally parallel to the resonator's axis and there are no nodes on either the input or output surfaces of the resonator.  

axisymmetric -- a cylindrical FEA model whose shape and material properties do not vary circumferentially around the model (e.g., transducers, boosters, and many cylindrical resonators). Variations in FEA amplitudes and stresses occur only in the axial and radial directions; circumferential variations are not permitted.  

flexure -- a vibration mode in which the stack vibrates transverse to its axis, similar to a bending beam.  

horn (probe, sonotrode) -- a resonant device that transmits ultrasonic energy to a load.  

loss -- power dissipated by the stack when running in air. High loss may indicate a potential reliability problem (e.g., fatigue, galling, transducer failure, flexure, etc.).  

nonaxial resonance -- any resonance other than the axial resonance.  

primary resonance -- the resonance that has the desired vibration mode. This is often an axial resonance but can also be flexural, radial, torsional, etc.  

nonprimary resonance -- any resonance that is not the primary resonance.  

stack -- an assembly of resonators. The usual plastic welding stack consists of a transducer (converter), booster, and horn. The usual medical transducer consists of a transducer and probe.  

transducer (converter) -- a resonant device that converts high frequency electrical energy into high frequency mechanical vibration. The material that performs the conversion may be either piezoelectric or magnetostrictive.

uniformity -- roughly, a ratio of two amplitudes on a specified resonator surface (usually the resonator face) that describes the degree to which the axial amplitude is the same over the specified surface. Uniformity is denoted by U. Generally, the optimum uniformity is 1.0 (i.e., 100%). (See Asymmetry.)  

unshaped resonator -- a resonator whose sides are essentially parallel to the stud axis. Unshaped resonators appear to have no gain.